
선형 회귀
변수의 관계를 활용한 예측
예측(Prediction)
주어진 정보를 활용해서 불확실한 미래를 대비
미래의 가능성이나 불확실성을 숫자로 계산해서 활용
결국 변수의 관계를 활용
관심 변수(반응 변수, 종속변수)
예측의 대상이 되는 변수
관심 변수에 관측치 간 차이가 존재
다양한 방법으로 관심 변수 속 차이를 확인 가능
설명변수(=독립변수)
관심 변수 속 차이를 설명할 수 있는 변수
관심 변수와 설명변수의 관계를 확인하여 예측에 활용
한 수치형 변수를 관심 변수로 지정
한 수치형 변수 요약 : 평균 계산
평균을 중심으로 관측치들이 흩어진 차이가 존재
조건부 평균(Conditional Mean)
특정 설명변수 조건과 일치하는 부분 관측치로 계산된 평균
범주형 설명 변수를 활용 : 그룹별 평균
수치형 설명변수를 활용 : 선형 회귀
한 범주형 변수를 설명변수로 지정
수준에 따라 그룹별 평균을 계산
각 관측치의 수준을 파악해 예측에 활용 가능
수치형 설명변수를 활용한 예측 전략
수치형 설명변수의 구간화를 통한 그룹별 평균 계산 가능
산점도와 상관 계수의 활용 사분면에서 관측치의 흩어진 패턴을 파악
상관계수 : 두 수치형 변수의 관계를 -1부터 1 사이의 숫자로 표현
일차함수
- 두 변수 X와 Y의 정비례 관계를 가정
X가 1씩 커질 때마다 Y는 b만큼 비례해서 변화
일차함수는 공간에서 직선으로 표현
추세선
일차함수를 활용하여 두 수치형 변수의 관계를 설명 가능
선형 회귀 모형의 개념
단순 선형 회귀(Simple Linear Regression)
수치형 관심 변수를 수치형 설명변수의 정비례로 설명하는 모형

X가 1씩 커질 때마다 Y는 b만큼 비례해서 변화
단, Y에는 X로는 설명할 수 없는 오차 E가 존재
설명변수 X와 회귀계수를 활용해서 관심 변수 Y를 예측 가능
선형 회귀모형의 적합
회귀 모형의 적합 두 변수 X와 Y의 관계식을 확인하는 과정
통계적으로 합리적인 추세선의 조건
최소 제곱 법(Least Squares Method)을 활용
X가 평균 정도 일 때는 Y도 평균 정도로 예측
따라서 모든 회귀 직선을 무게 중심(X, Y)을 지남
추정된 회귀계수 β0, β1와 X를 활용한 예측 값과 실제 값 Y의 전반적인 차이가 적음
최적의 직선의 기울기 β1을 데이터로부터 계산
추정된 회귀 계수와 상관 계수의 관계
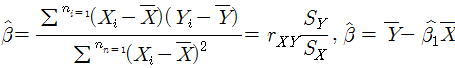
회귀 직선의 기울기 β1는 두 변수의 상관계수에 비례
'데이터분석 > 기초' 카테고리의 다른 글
| [데이터분석] 데이터 분석의 꽃 통계 8 (2) | 2021.12.27 |
|---|---|
| [데이터분석] 데이터 분석의 꽃 통계 7 (2) | 2021.12.21 |
| [데이터분석] 데이터 분석의 꽃 통계 5 (0) | 2021.12.19 |
| [데이터분석] 데이터 분석의 꽃 통계 4 (2) | 2021.12.18 |
| [데이터분석] 데이터 분석의 꽃 통계 3 (0) | 2021.12.17 |








최근댓글